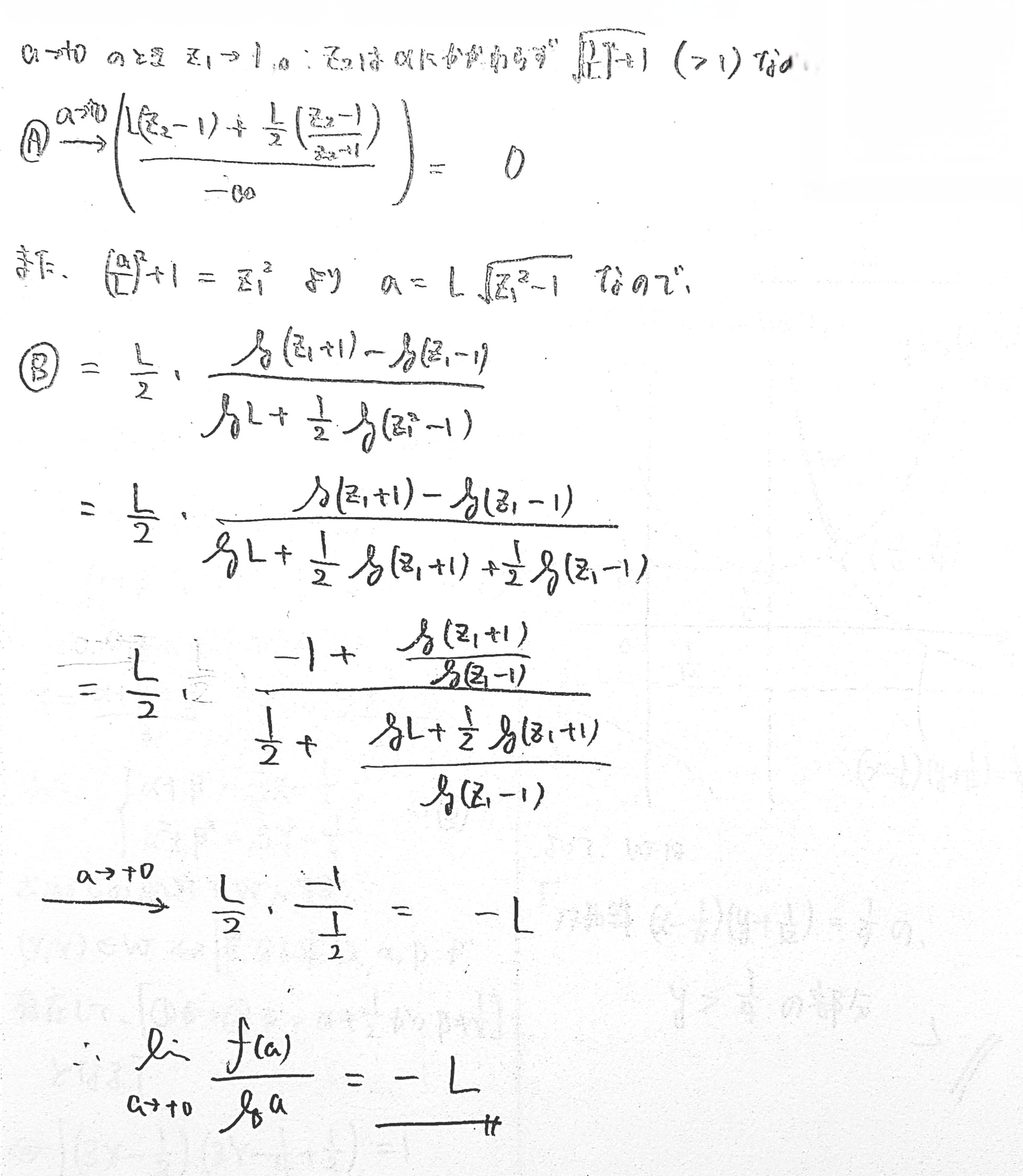$L$ を正定数とする。座標平面の $x$ 軸上の正の部分にある点 $P(t,0)$ に対し，原点 $O$ を中心とし点 $P$ を通る円周上を，$P$ から出発して反時計回りに道のり $L$ だけ進んだ点を $Q(u(t),v(t))$ と表す。

(1)　$u(t),\ v(t)$ を求めよ。

(2)　$0 < a < 1$ の範囲の実数 $a$ に対し，積分
$f(a)=\displaystyle\int_a^1 \sqrt{\{u'(t)\}^2+\{v'(t)\}^2}dt$
を求めよ。

(3)　極限 $\displaystyle\lim_{a\to+0}\frac{f(a)}{\log a}$ を求めよ。