東大理系数学 2013-2
$a$ を実数とし,$x>0$ で定義された関数 $f(x),g(x)$ を次のように定める。
$f(x)=\dfrac{\cos x}{x}$
$g(x)=\sin x+ax$
このとき $y=f(x)$ のグラフと $y=g(x)$ のグラフが $x>0$ において共有点をちょうど3つもつような $a$ をすべて求めよ。
解答例
$a$ について解ける形をしているので、定数分離を行う。
式の見た目に反し、微分後は綺麗になる。
(逆に言えば【微分後の式】の不定積分が解けるというのは、少し興味深いかもしれない)
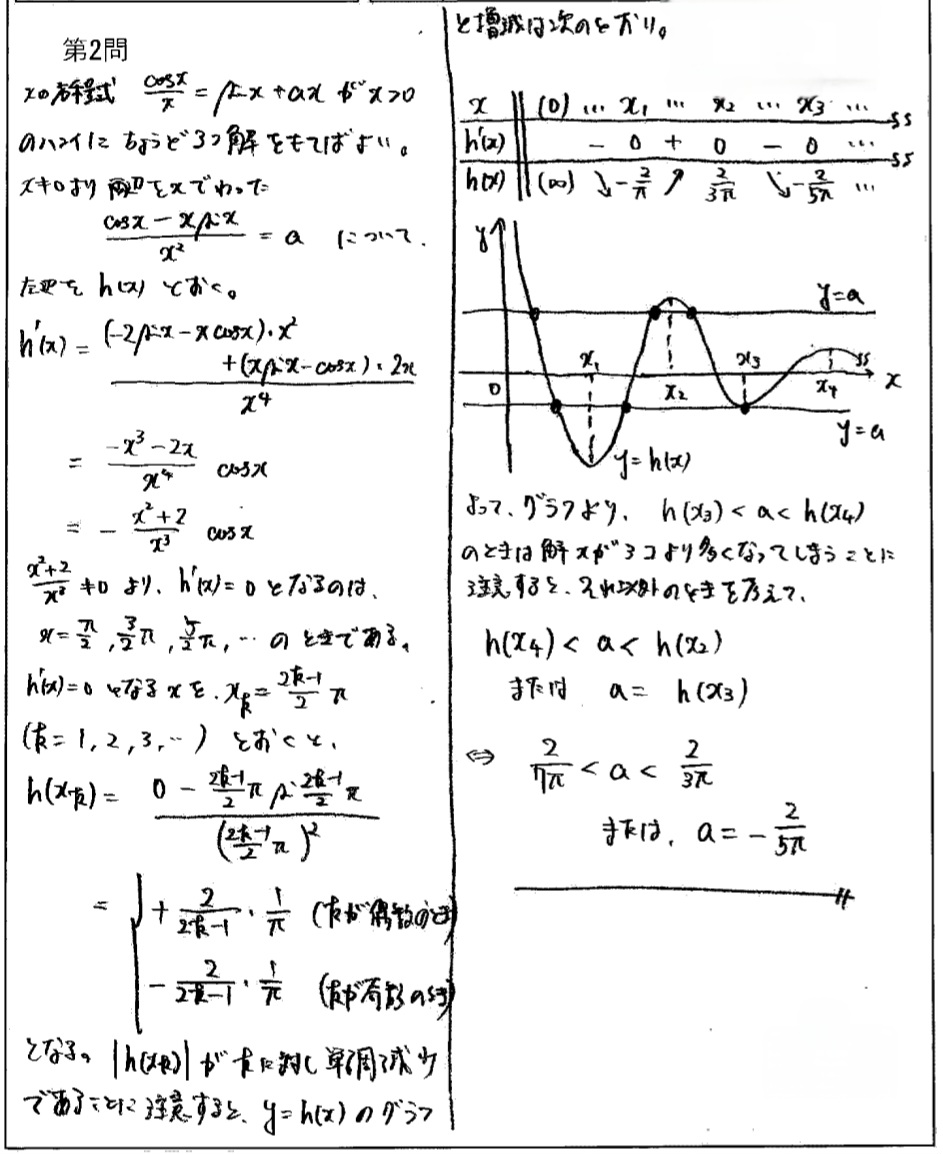
> 所々日本語が怪しい点は目をつむってください...。
動く図解
実際問題文を直訳してグラフを描くと前者のようになるが、非直感的で分かりづらい。だからこそ、定数分離が必要になる。
(※後者の「解の個数」については、境界条件の実装が面倒だったので、$a=-\frac{2}{5\pi}$ とかにしても解は3個にならなくなっています)
問題の背景
「解の個数」系の問題は典型問題としてほぼ研究し尽くされているように感じます。一般的な大学入試における問題はほぼ既出のことが多く、新規性を持った出題はなかなか見かけません。本問もやるべき変形を行えば、答えにたどり着けると思います。
今回の解説では、「グラフより」の許容範囲について考察していきます。
問題の解答でよく見かける「グラフより」というと、次のようなもの(画像参照)が思いつくでしょう。3つ目はいったん置いておくと、最初の2つは「区間ごとにおける単調性を可視化している」点で通底しています。ここには特に問題は無く、実際これを今読んでいる方々も当たり前に使ってきた手段だと思われます。
3つ目はというと、逆関数の極限を定数分離と見なす考え方を図示したものです。こんな解答はいいのかと疑問に感じる人もいるかもしれませんが、全く問題ないと思います。(これに似た方法が2021-5で利用できます)
(※実際これを疑いだした場合、「対数の極限は極限の対数」とかも怪しくなってきます。ですが、この事実は当然のように使っているはずです。例えば $\displaystyle\lim_{x\rightarrow+0}x^x$ を求めるときなど... なお、厳密な証明には $\varepsilon-\delta$ 論法を要します。)
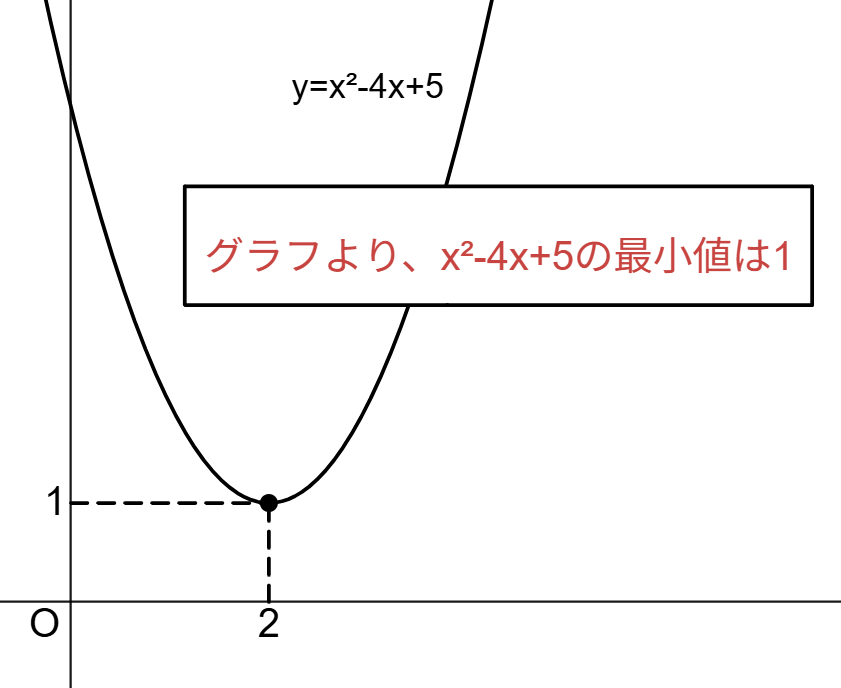
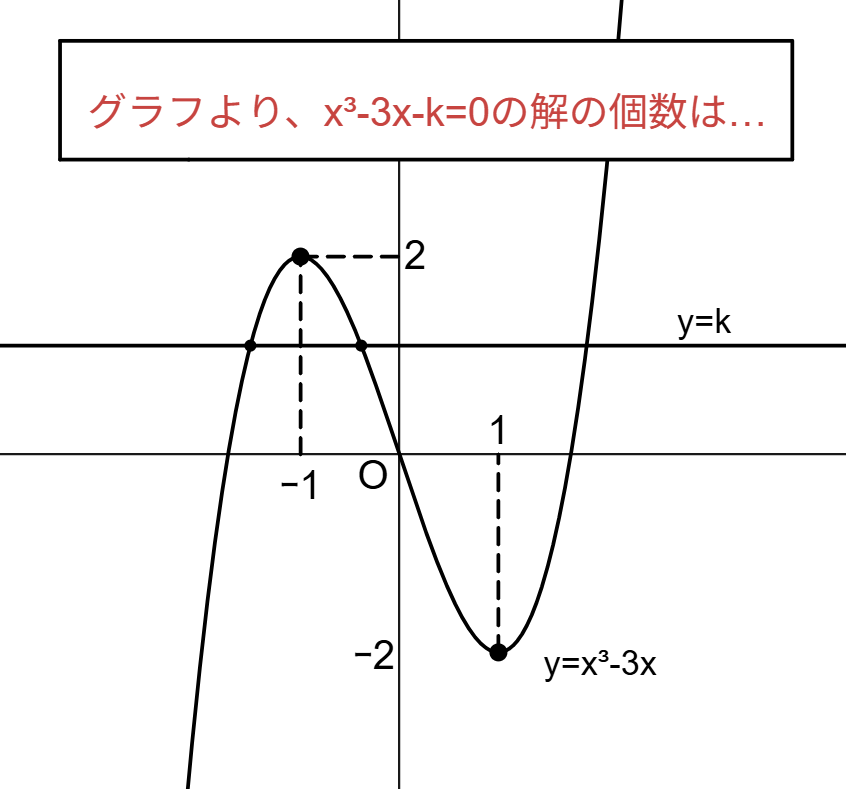
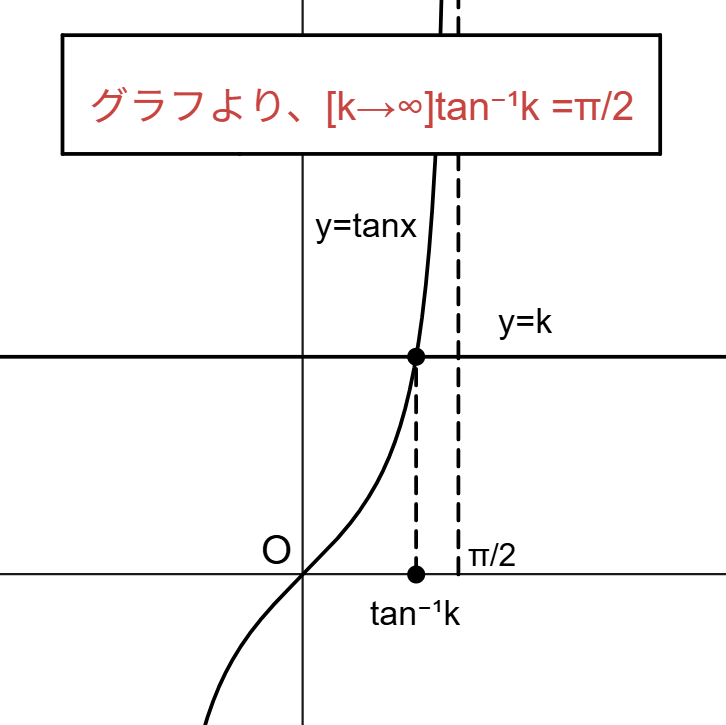
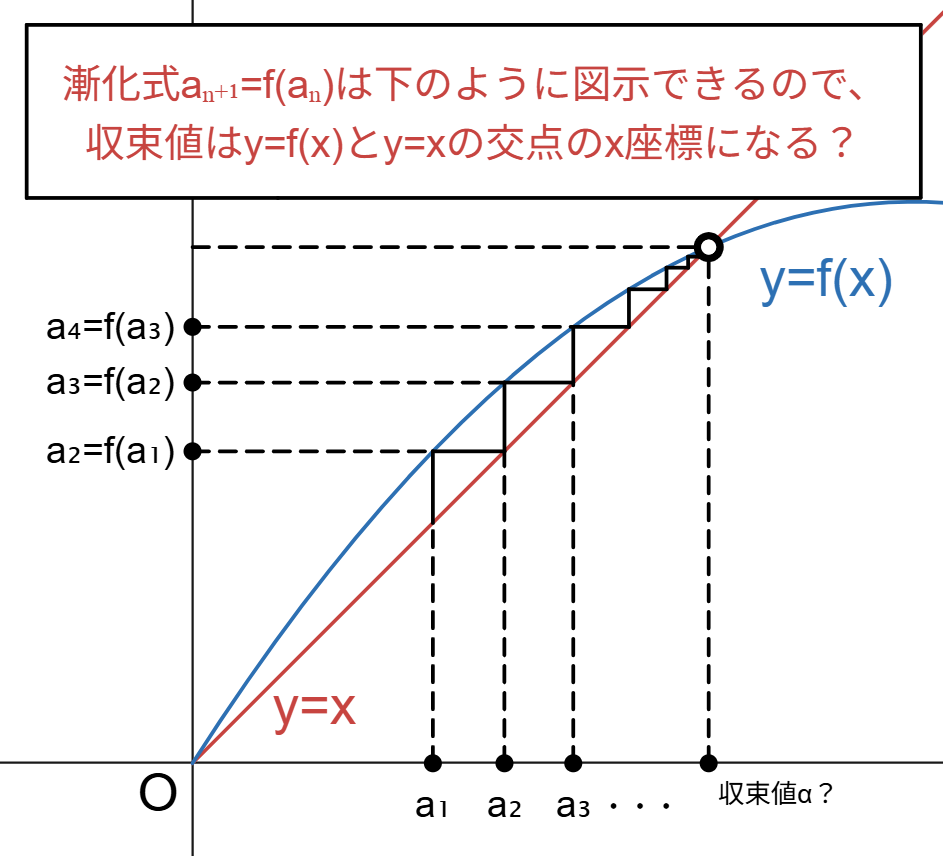
ただし、「グラフより」が通用しない場面もあります。その最たる例は再帰漸化式の極限の禁じ手でしょう。(画像参照)
これが上記の例と決定的に異なるのは、図に描かれた点や線の位置関係に根拠がない点です(特に極限での振る舞い)。グラフはあくまでも事実の視覚化にすぎず、何でも読み取れるわけではないことに注意しましょう。
類題紹介
【問題の背景】の内容を踏まえた問題です。
$a$ を正の実数とし,$x>0$ で定義された関数 $f(x),g(x)$ を次のように定める。
$f(x)=\dfrac{\cos x}{x}$
$g(x)=\sin x+ax$
(1) $y=f(x)$ のグラフと $y=g(x)$ のグラフが $x>0$ において共有点をちょうど1つもつような $a$ の範囲を求めよ。
(2) $a$ が(1)の範囲にあるとき、$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の座標を $(x_a,y_a)$ とおく。次の3つの極限をそれぞれ求めよ。
$$\lim_{a\rightarrow\infty}x_a\qquad\lim_{a\rightarrow\infty}ax_a^2\qquad\lim_{a\rightarrow\infty}\frac{ax_a^2-1}{x_ay_a-1}$$
(東大2013 魔改造)
ここからは一筋縄ではいかない問題を集めてみました。
(東工大2013)
(1) $k$ を実数の定数とし,$f(x)=xe^{-x}$ とおく。方程式 $f(x)=k$ の異なる実数解の個数を求めよ。ただし,$\lim_{x\to\infty}f(x)=0$ を用いてもよい。
(2) $xy e^{-(x+y)}=c$ をみたす正の実数 $x,y$ の組がただ1つ存在するときの実数 $c$ の値を求めよ。
(3) $xy e^{-(x+y)}=\dfrac{3}{e^4}$ をみたす正の実数 $x,y$ を考えるとき,$y$ のとりうる値の最大値とそのときの $x$ の値を求めよ。
(北大2023)