東大理系数学 2019-1
次の定積分を求めよ。
$\displaystyle \int_0^1 \left(x^2+\frac{x}{\sqrt{1+x^2}}\right)\left(1+\frac{x}{(1+x^2)\sqrt{1+x^2}}\right)dx$
方針、略解
中身を展開して積分しましょう。多項式の積分,微分形接触,tan置換などを適宜利用します。
問題の背景
まさかの「ただ積分するだけ」として話題になった問題です。特に技巧的な方法はあまり必要なく、本当に計算問題です。とはいえ、そもそも東大の積分(体積ではなく、ただ積分計算をさせるだけの問題)は、そのほとんどは工夫はいらず、淡々と複雑な計算をさせるものばかりで、むしろ数学的意味を考えるのが無駄なものも多いです(2021-3,2014-3など)。そのため、本問もこれらのような、計算力を試す問題として出されたのでしょう。
ついでなので、この手の高度典型の積分一覧を示しておきます。これらの導出を網羅すればあらゆる問題をオーバーキルできるでしょう。
以下では、$y=\tan x(|x| < \frac{\pi}{2})$の逆関数を$\tan^{-1}x$のように書く。他も同様。
★Level1:基本
$$(1) \ \int\frac{dx}{x^2+a^2}=\frac1a\tan^{-1}{\frac{x}{a}}+C$$
$$(2) \ \int\frac{dx}{x^2-a^2}=-\frac1a\tanh^{-1}{\frac{x}{a}}+C$$
$$(3) \ \int\frac{dx}{(x^2+a^2)^2}=\frac{1}{2a^3}\left(\tan^{-1}{\frac{x}{a}}+\frac{ax}{a^2+x^2}\right)+C$$
$$(4) \ \int\frac{dx}{(x^2-a^2)^2}=\frac{1}{2a^3}\left(\tanh^{-1}{\frac{x}{a}}+\frac{ax}{a^2-x^2}\right)+C$$
$$(5) \ \int\frac{x}{x^2\pm a^2}dx=\frac{1}{2}\log{\left|x^2\pm a^2\right|}+C$$
$$(6) \ \int\frac{x}{(x^2\pm a^2)^2}dx=-\frac{1}{2(x^2\pm a^2)}+C$$
$$(7) \ \int\sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}-a^2\cos^{-1}{\frac{x}{a}}\right)+C$$
★★Level2:標準
$$(8) \ \int\frac{dx}{\sqrt{x^2+ a^2}}=\sinh^{-1}{\frac{x}{a}}+C$$
$$(9) \ \int\frac{dx}{\sqrt{x^2- a^2}}=\cosh^{-1}{\frac{x}{a}}+C$$
$$(10) \ \int\frac{dx}{\sqrt{a^2- x^2}}=-\cos^{-1}{\frac{x}{a}}+C$$
$$(11) \ \int\sqrt{x^2+a^2}dx=\frac{1}{2}\left(x\sqrt{a^2+x^2}+a^2\sinh^{-1}{\frac{x}{a}}\right)+C$$
$$(12) \ \int\sqrt{x^2-a^2}dx=\frac{1}{2}\left(x\sqrt{x^2-a^2}-a^2\cosh^{-1}{\frac{x}{a}}\right)+C$$
...しかしこの問題、積分するだけなのだとしたら、なぜ因数分解された形で、しかも左の項が中途半端にまとめられた状態で出題したのでしょうか?
ということで、ここからはこの問題ができるまでの経緯の予想を話します。【あくまで予想なので、真相は作問者のみぞ知るということに注意】
"真の"(?)問題背景
突然ですが、こんな問題を紹介しましょう。
(ただし、$P$は$y < \frac12x^2$かつ$|x|\leqq1+\frac{1}{\sqrt2}$の範囲にあるとする。)
下のように、法線上に点$P$があるイメージさえつかめれば、あとはベクトル的に処理できます。
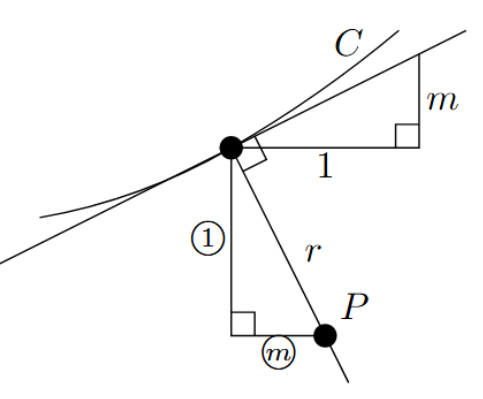
(↑今回は距離$r=1$,傾き$m=t$ ($t$は接点の$x$座標) )
$r,m,t$を上記のように設定すると、$$\overrightarrow{OP} = \begin{pmatrix}t\\ \frac12t^2\end{pmatrix} + \frac{r}{\sqrt{m^2+1}}\begin{pmatrix}m\\-1\end{pmatrix} = \begin{pmatrix} t+\frac{t}{\sqrt{t^2+1}} \\ \frac12t^2-\frac{1}{\sqrt{t^2+1}}\end{pmatrix} $$
よって、$P$は上記のように媒介変数表示された曲線上を動きます。(ただし$|t|\leqq1$)
では、ここでこんな質問をしてみましょう。
$P$は$x$軸よりも下を動きますから、(∵$y$座標が常に負)
$\overrightarrow{OP} = \begin{pmatrix}x(t)\\y(t)\end{pmatrix}$ とおくと、計算すべき面積は、$\displaystyle{S=-\int_{x(-1)}^{x(1)}ydx}$になります。
置換積分を使って変形してみましょう。
$$\begin{align} S&=-2\int_0^{x(1)}ydx\qquad(\because 対称性)\\ &=-2\int_0^1y(t)\frac{dx}{dt}dt\qquad(積分変数をxからtへ変更)\\ &=-\int_0^1\left(t^2-\frac{2}{\sqrt{1+t^2}}\right)\left(1+\frac{1}{(1+t^2)\sqrt{1+t^2}}\right)dx\\ &=\cdots(以下省略) \end{align}$$
すると、本問とかなり類似した式を得ます。積分変数を同じにして比較してみましょう。
何が言いたいのかというと、本問の式は、見た目が非常に$\int y \frac{dx}{dt}dt$に似ているので、作問時点では求積問題だったのでは?ということです。ここからは完全に予想になってしまうのですが、おそらく本問は次のように作問されたのかなと思います。
ボス問級の求積問題を作ろう!
↓
放物線との距離を考える問題ができた!それなりに良問になりそう
↓
と思ったらほかの問題で後半4,5,6問が埋まってしまった...
↓
1番級のものに改題するために、計算の部分だけ出そうかな
↓
無駄な符号は消して、あとは知識勝負になりがちな$\int\frac{1}{\sqrt{1+x^2}}dx$も、普通のtan置換に変えておくか...
↓
大問1として出題される
類題紹介
せっかくなので、「曲線との距離が一定になる」系の問題を置いておきます。ちなみに3次元の場合にはその内部を「管状近傍」と呼ぶことがあるそうです。
また,点 $Q(s,\ t)$ は法線 $\ell$ 上にあり,$PQ=1$ かつ $t < a$ を満たすとする。
(1) 導関数 $f'(x)$ を求めよ。また,法線 $\ell$ の方程式を求めよ。
(2) $s$ および $t$ を $a$ を用いて表せ。また,極限 $\displaystyle\lim_{a\to+0}s$ を求めよ。
(3) $n$ を $0$ 以上の整数とする。$a\to+0$ のとき,$\frac{t}{a^n}$ が収束するような $n$ の値をすべて求めよ。また,そのときの極限値をそれぞれ求めよ。
(筑波大?年度不明)
さらに、曲線$D$に平行移動、原点に関する回転移動、またはその両方を施して得られる図形を$E$とする。
$C$と$E$が少なくとも$1$つの共有点を持つように$E$が動くとき、$E$が通過しうる領域全体の面積を求めよ。
(自作問題、激ムズ注意)
ここからは積分をひたすら集めていきます。