ブックマーク

東大理系数学 2024-5

座標空間内に3点$A(1,0,0),B(0,1,0),C(0,0,1)$をとり、Dを線分ACの中点とする。三角形ABDの周および内部を$x$軸の周りに1回転させて得られる立体の体積を求めよ。

方針、略解

$x=t$での$x$軸最近点、最遠点距離を求める。場合分けの境界に注意。

$$\frac{\pi}{9}$$

動く図解

(gif画像です。画質はご愛敬)

問題の背景

空間内で図形を回転させるとき、最遠点と最近点を追跡するというのはよくある作戦です。今回も定石通り、三角形の切断面内での形を把握できれば解答にまっすぐ進めると思います。ただし、場合分けの境界が三角形の頂点とは限らないことには注意が必要です。

ここでは、今回の問題をより拡げた視点を考えたいと思います。次の重要事実を確認します。

①直線上のあらゆる点から、直線を含まないある平面に垂線を下ろしたとき、垂線の足は直線を描く。

②直線の回転体は、円柱、円錐、そして「一葉双曲面」のいずれかになる。（直線が回転軸と垂直な場合を除く）

①について：
証明は容易です。「直線の正射影は直線」と言っていることは同じです。

②について：
一葉双曲面というのは、双曲線の（焦点を通らない対称軸に関する）回転体のことです。②はつまり、「直線の回転体を考えたとき、$z=t$での回転軸との距離は、$\sqrt{tの2次式}$で表されるよ」って意味です。画像やリンクから動きを見てみると分かりやすいかと思います。

（Desmosリンク：https://www.desmos.com/3d/3ytz2hfgqm）

以上二つを踏まえて今回の問題を眺めてみましょう。最遠点と最近点は、三角形の端または回転軸上の$x=t$の点から下ろした垂線の足なので、①より線分をつなげたものになります。すると②よりこれの回転体の体積を求めるには、$\sqrt{（tの2次式）}$の2乗に$\pi$を書けたものを積分していく(円環の面積計算)ことになるので、多項式の積分で済むことが一目瞭然です。

類題紹介

底面の半径1、母線の長さ$\sqrt2$の円錐を、頂点Oを中心として、側面が平面上をすべらないように出発地点Aから転がし、頂点Oのまわりをちょうど1周させる。このとき、円錐の底面の円周が通過してできる曲面の面積を求めよ。

(都立立川)※高校入試

半球

半径$r$,高さ$h(>r)$の直円錐を，頂点を固定して平面状を図のようにすべることなくころがす。
円錐の中心軸が一周してもとの位置に戻るとき，円錐が通過する部分の体積を求めよ。

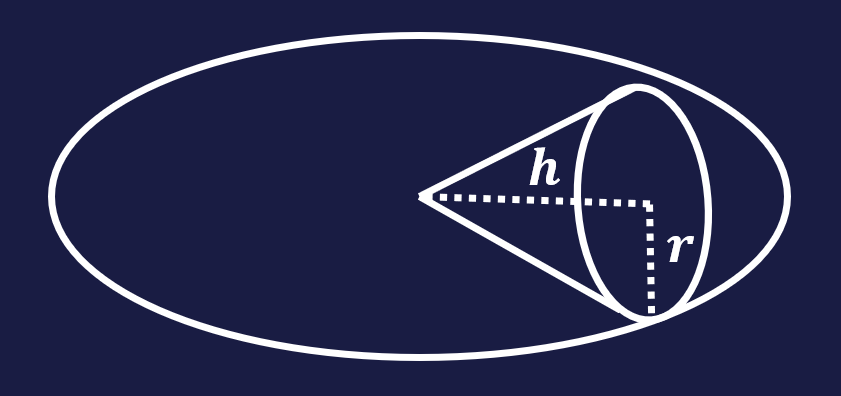
(東京電機大)

こちらは球を帯状に切り出したものと円錐面から成るが、分けて考えるとむしろ計算は重くなる。いつでも初等幾何的計算が賢いとも限らない。

一辺の長さが1の立方体を、中心を通る対角線のうちの一本を軸として回転させたとき、この立方体が通過する部分の体積を求めよ。
(東工大1993)

座標空間内の2点 $O(0,0,0),\ A(2,0,0)$ に対し，
$\displaystyle 2AP \le OP \le AP + \frac{2\sqrt{5}}{3}$
をみたす点 $P$ 全体からなる立体を $K$ とする。$K$ の体積を求めよ。
(東大模試)

等号成立条件が、アポロニウス円と双曲線の幾何定義

$(x^2+y^2+z^2+8)^2\leqq36(x^2+y^2)$を満たす領域の体積を求めよ。
(パトナム数学コンペ2006)

二乗和を回転軸からの距離の二乗とみる（ちなみにこの式はトーラスを表す）

$xyz$空間内の動点$P$を考える。
$P$は$z\leqq0$の部分では最大秒速$a$メートルで、$z>0$の部分では最大秒速$1$メートルで動けるものとする。
$P$がはじめに原点$(0,0,0)$にあるとき、その1秒後までに$P$が到達しうる範囲の体積を求めよ。
ただし、$a>1$とする。　　(東工大2001)

上側の様子をイメージしづらい。難問。

▲