東大理系数学 2025-3
平行四辺形$ABCD$において, $\angle ABC=\frac{\pi}{6}, \ AB=a, \ BC=b, \ a\leqq b$ とする。次の条件を満たす長方形$EFGH$を考え、その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ辺$EF,FG,GH,HE$上にある。
ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、$S$を$a,b,\theta$を用いて表せ。
(2)$S$の取り得る値の最大値を$a,b$を用いて表せ。
方針、略解
(1)角度追跡ののち、底辺×高さ。答えの形は結構人によりばらけそう。
(2)三角関数の合成。簡単に計算する方法を後述します。
動く図解
問題の背景
(2)はベクトルの内積を利用すると明快な解答が作れます。以下では少し丁寧に清書したものを掲載します。
加法定理等を用いると、$S=\frac{\sqrt3}{4}a^2\cos2\theta+\frac{2b^2-a^2}{4}\sin2\theta+\frac{ab}{2}$と変形できる。
この式は、1,2項目を内積と見なすことにより、次のように変形できる。
$$S \ = \ \frac14\Bigg\{\underline{\begin{pmatrix}\sqrt3a^2\\2b^2-a^2\end{pmatrix}}_{(これを\overrightarrow{OX}とする)}\cdot\underline{\begin{pmatrix}\cos2\theta\\ \sin2\theta\end{pmatrix}}_{(これを\overrightarrow{e}とする)}\Bigg\}+\frac{ab}{2} \ = \ \frac14(\overrightarrow{OX}の\overrightarrow{e}への正射影の符号付き長さ)+\frac{ab}{2}$$
ここで、$0\leqq2\theta\leqq\frac{\pi}{3}$より、$P(\overrightarrow{e})$は単位円上の第一象限内の$y\leqq\sqrt3x$の部分を動く。また、$(\overrightarrow{OX}の傾き)=\frac{2b^2-a^2}{\sqrt3a^2}\geqq\frac{1}{\sqrt3}(\because a\leqq b)$より、$X$は第一象限の$y\geqq\frac{1}{\sqrt3}x$の部分を動く。
よって、$X$が直線$l:y=\sqrt3x$の上下どちら側にあるかで場合分けが生じる。(図を参照)
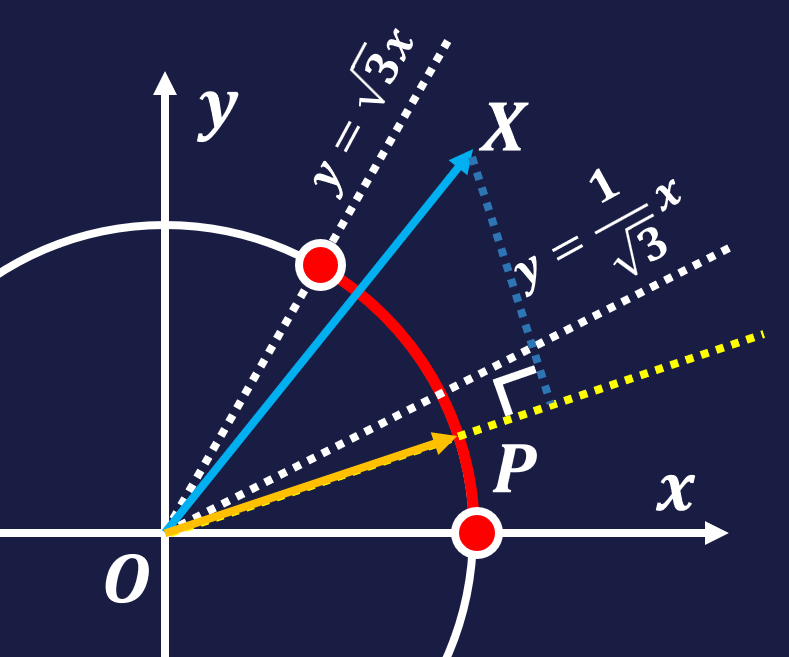
(i)$X$が$l$の下側または$l$上にあるとき、当然$\overrightarrow{OP} /\!/ \overrightarrow{OX}$で$S$の最大値が達成される。 このときの$S$を$S_{\max}$とすると、$S_{\max}=\frac14|\overrightarrow{OP}|+\frac{ab}{2}=\frac12\sqrt{a^4-a^2b^2+b^4}+\frac{ab}{2}.$ なお、$X$が$l$の下側にある条件は、$(\overrightarrow{OX}の傾き)\leqq \sqrt3$より計算すると、$b\leqq \sqrt2a$である。
(ii)$X$が$l$の上側または$l$上にあるとき、$\overrightarrow{OP}=\begin{pmatrix}\frac12\\\frac{\sqrt3}{2}\end{pmatrix}$で最大値となる。 よってこのときの最大値を計算すると、$S_{\max}=\frac{\sqrt3}{4}b^2+\frac{ab}{2}.$ $X$が$l$の上側にある条件は、$b\geqq\sqrt2a$である。
以上より、 $$ S_{\max}=\begin{cases} \frac12\sqrt{a^4-a^2b^2+b^4}+\frac{ab}{2} \quad (a\leqq b\leqq\sqrt2aのとき)\\ \frac{\sqrt3}{4}b^2+\frac{ab}{2}\quad (b\geqq \sqrt2aのとき) \end{cases} $$
三角関数の線形結合を内積と見なすのがミソです。淡々とした計算とは打って変わって図形的な解き方をすることができ、比較的ミスが起こりにくいです。
類題紹介
辺の長さが 1 および $a$ の長方形 $ABCD$ と、これに図のように外接している正三角形 $PQR$ がある(長方形の辺が三角形の辺上にある場合も含む)。 $\angle BAQ = \theta$ とおく。ただし、 $\frac{\pi}{6} \le \theta \le \frac{\pi}{3}$とする。
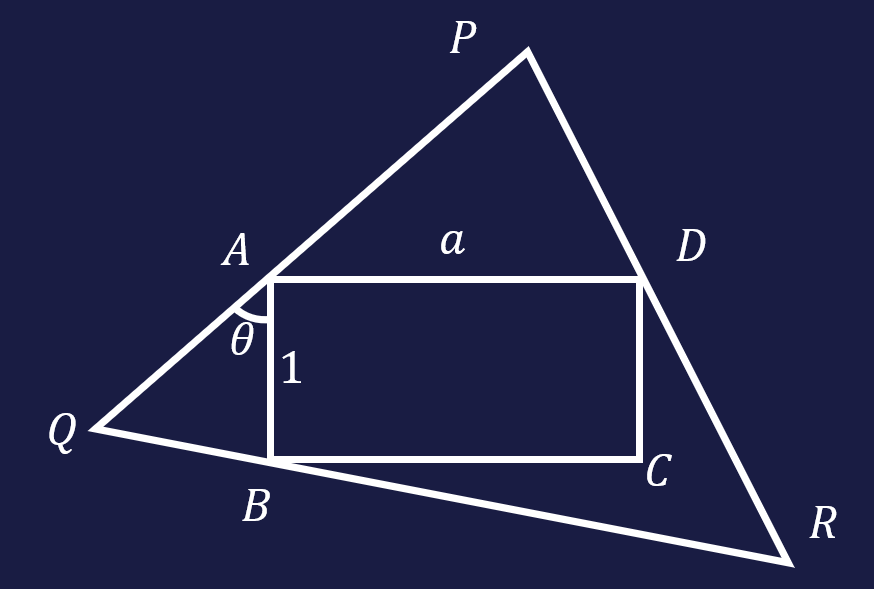
(1) 正三角形の 1 辺の長さ $y$ を求めよ。
(2) $y$ の最大値および最小値を求めよ。
(出典不明、入試問題)$f(\theta) = a\sin^{2}\theta + b\cos^{2}\theta + c\sin\theta\cos\theta$
$(0 \le \theta \le \frac{\pi}{2})$
を考える。$f(\theta)$ の最大値を $M$,最小値を $m$ とし,$f(\theta)$ が最大値 $M$ をとるときの
$\theta$ を $\theta_{0}$ とする。次の問いに答えよ。
(1)$a=b$のとき、 $\theta_0$ の値を求めよ。
(2) $a > b$ かつ$M-m=c$であるとする。$c$ を$a,b$を用いて表し、$\sin\theta_0$の値を求めよ。
(4) $a < b$ かつ$M-m=c$であるとする。$\sin\theta_0$の値を求めよ。
(早慶模試)
$a$を正の実数とするとき,次の問いに答えよ。
(1)辺の長さが 1,他の 2 辺のうち 1 辺の長さが $a$ である三角形のなかで, 面積が最大である三角形の残りの 1 辺の長さを $a$ を用いて表せ。
(2)辺の長さが 1,他の 2 辺のうち 1 辺の長さが $a$ である四角形のなかで, 面積が最大である四角形の残りの 1 辺の長さを $a$ を用いて表せ。
(出典不明、医学部の入試問題)平面上に四角形ABCDがあり、$AB = a,\quad BC = b,\quad \angle A = \theta$とする。
条件$\angle A = \angle B = \angle C,\qquad \frac{\pi}{3} < \theta < \frac{\pi}{2},\qquad b < a < \frac{b}{2\cos\theta}$のもとで、以下の問に答えよ。
(1)$CD=c$を$a,b,\theta$を用いて表せ。
(2)$ a, b $ を固定して,$\theta$ が $\frac{\pi}{3} < \theta < \frac{\pi}{2}$ を動くときの$ c $ の最小値を求めよ。
(出典不明、入試問題)